SNT – Séquence 2 : Activité 2
Pour communiquer et traiter des informations, les ordinateurs et appareils numériques utilisent des langages de base comme le binaire (0 et 1) et des systèmes de conversion comme l'hexadécimal. Les données transmises sur Internet, les adresses IP, ou les fichiers que nous utilisons quotidiennement sont souvent exprimés en bits, octets et leurs multiples. Il est donc essentiel de comprendre comment convertir ces données dans différents formats pour mieux appréhender le fonctionnement des systèmes informatiques.
Objectifs :
- Savoir convertir des octets en bits.
- Comprendre les bases du calcul binaire et hexadécimal.
- Savoir faire des conversions de nombres binaires en hexadécimal ou en décimal.
- Comprendre l'importance de ces conversions dans le traitement et la transmission de données sur Internet.
Partie 1 : Conversion Octets et Bits
Nous allons commencer par la conversion entre octets et bits, des unités de base utilisées pour mesurer et stocker les données numériques.
Rappels théoriques :
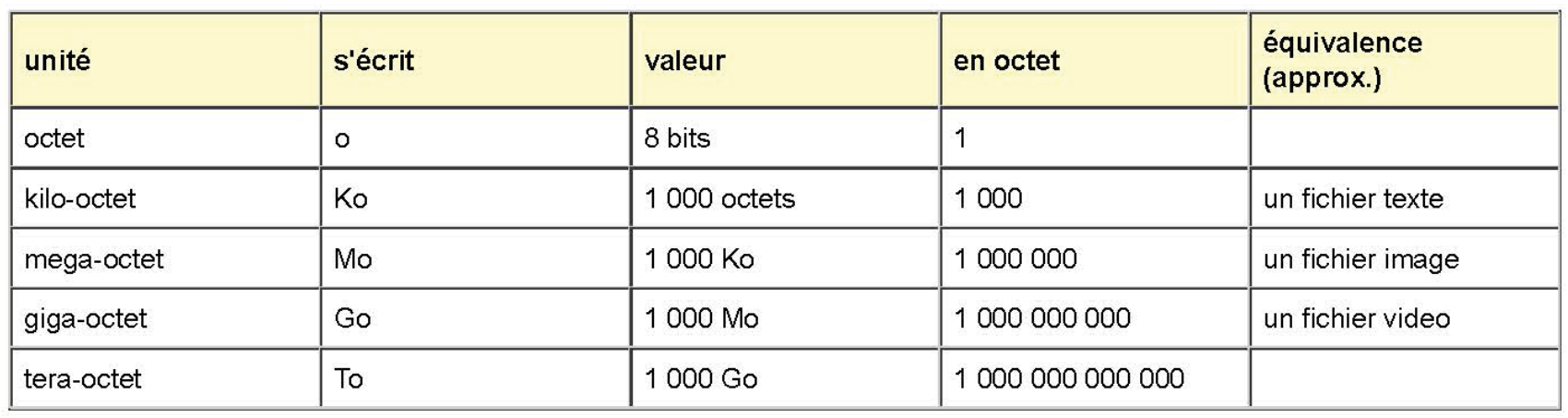
- 1 octet = 8 bits.
- Les multiples courants sont le kilo-octet (KB), le méga-octet (MB), le giga-octet (GB), et ainsi de suite.
Exercice pratique : Convertissez les données suivantes en bits :
- 5 octets = ?
- 15 octets = ?
- 2,5 kilo-octets (KB) = ?
- 1 méga-octet (MB) = ?
Attention : les valeurs données ci-dessous ne sont pas rigoureuses, mais approchées. Si l'on voulait être rigoureux, il faudrait utiliser 1024, et non 1000, comme multiplicateur entre chaque unité.

Si vous avez besoin d'aide ou de plus de ressources : cliquez ici et lisez !
Vérification : Une fois les conversions effectuées, échangez vos réponses avec vos voisins pour vérifier si elles sont correctes, puis avec M. SALAH, avant de passer à la partie 2.

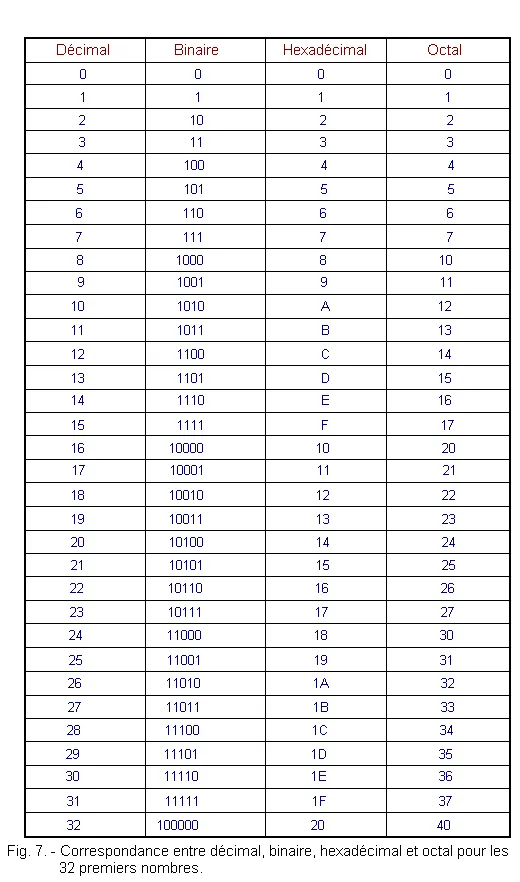
Partie 2 : Conversion Binaire <> Décimal <> Hexadécimal
Le binaire est le langage natif des ordinateurs, tandis que l'hexadécimal est un format compact et pratique utilisé par les programmeurs pour lire et écrire les valeurs binaires. Vous apprendrez à convertir des nombres binaires en hexadécimal et vice-versa.
Rappels théoriques :
- Système binaire : utilise les chiffres 0 et 1 (base 2).
- Système hexadécimal : utilise les chiffres de 0 à 9 et les lettres de A à F pour représenter les valeurs de 0 à 15 (base 16).
Exercice pratique : Convertissez !
1. Convertissez le nombre (65)10 en binaire et en hexadécimal.
2. Convertissez le nombre décimal (128)10 en binaire et en hexadécimal.
3. Convertissez le nombre binaire (10101010)2 en décimal et en hexadécimal.
4. Convertissez le nombre binaire (11111111)2 en décimal et en hexadécimal.
5. Convertissez le nombre hexadécimal (AF)16 en binaire et en décimal.
6. Convertissez le nombre hexadécimal (C9)16 en binaire et en décimal.